CHANGES IN VERSION 2.16 SINCE VERSION 2.15.2
Major changes
- P2-DPOP & MPC-DisWCSP4 now support maximization problems and problems with negative costs/utilities (request by Sankarshan Damle).
- Max-Sum now supports synchronous, round-based execution (in addition to asynchronous execution). Preliminary experimental results show that the asynchronous version outperforms the synchronous version on all performance metrics (see below).
Minor changes
- Fixed a NumberFormatException in P-DPOP and P3/2-DPOP (reported by Sankarshan Damle), which now only support AddableBigInteger utilities.
- The CATS parser now reports an error when more dummy goods are encountered than announced (issue reported by Sankarshan Damle).
- The JaCoPxcspParser now truncates decimal values to integers instead of throwing a NumberFormatException (issue reported by Sankarshan Damle).
- Fixed a bug in Max-Sum following which messages were skipped instead of delayed if received before the factor graph message.
- Fixed a bug in the factor graph DOT representation: names of function nodes and variable nodes could clash.
- Fixed serialization bugs in MPC-Dis[W]CSP4, which did not work with TCP pipes.
- Fixed a bug following which P3/2-DPOP would not assign any value to any variable on infeasible problems.
- Fixed a bug following which using AddableBigInteger for utilities/costs resulted in algorithms reporting very large instead of infinite utilities/costs on infeasible problems.
- Added warnings about truncations when attempting to parse decimal values from XCSP into integers.
- Added asserts to check for integer overflows in AddableInteger.
Experimental results: Max-Sum sync vs Max-Sum async
The difference in performance between the synchronous and the asynchronous versions of Max-Sum is influenced by the following competing factors:
- In Max-Sum async, each node in the factor graph responds to all its neighbors upon receiving any single message from any neighbor, unlike in Max-Sum synch, in which the node waits until it has received a message from each of its neighbors to respond to all. This should result in Max-Sum async exchanging on the order of d times more messages than Max-Sum sync, where d is the degree of the factor graph.
- In Max-Sum async, once a function node in the factor graph has exhausted its number of iterations, it still continues answering received messages from variable nodes that may still be running, in order to not prevent them from exhausting their numbers of iterations. This should further result in Max-Sum async exchanging more messages than Max-Sum sync.
- In Max-Sum async, a performance improvement has been implemented following which a node in the factor graph does not respond to a received message if it has not changed since the last message received from the same neighbor, since this would result in the same response. This performance improvement cannot be implemented for Max-Sum sync, since each node in the factor graph needs to wait for 1 message from each of its neighbors before it can complete its iteration. This should result in Max-Sum async exchanging fewer messages than Max-Sum sync.
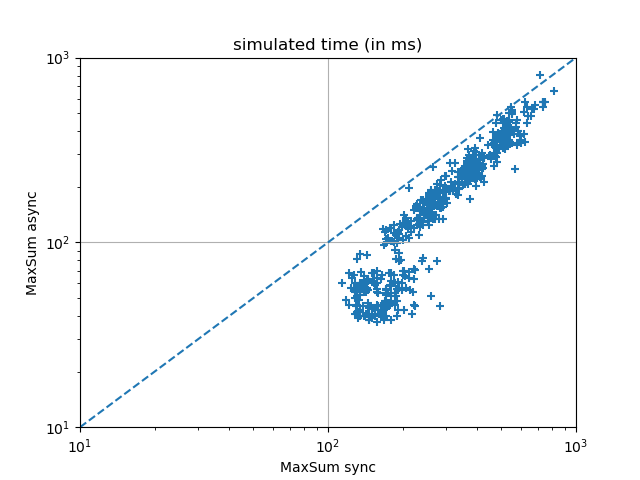
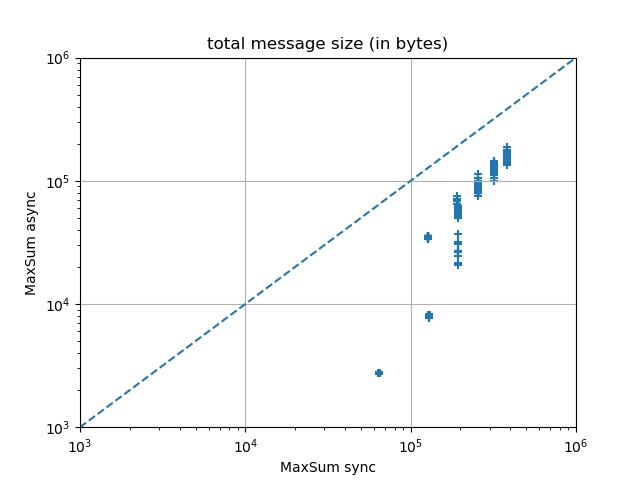
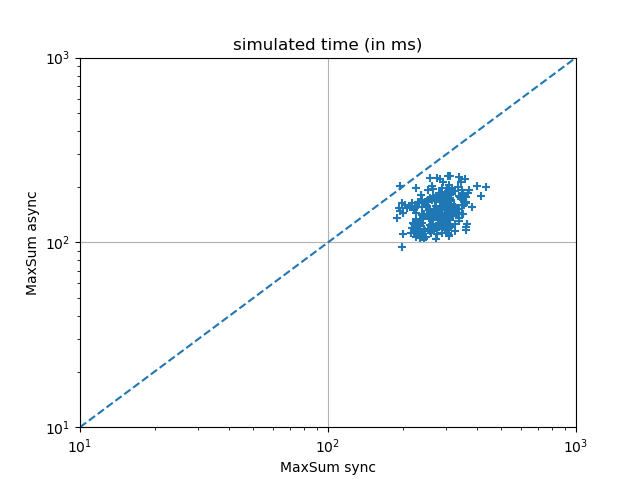
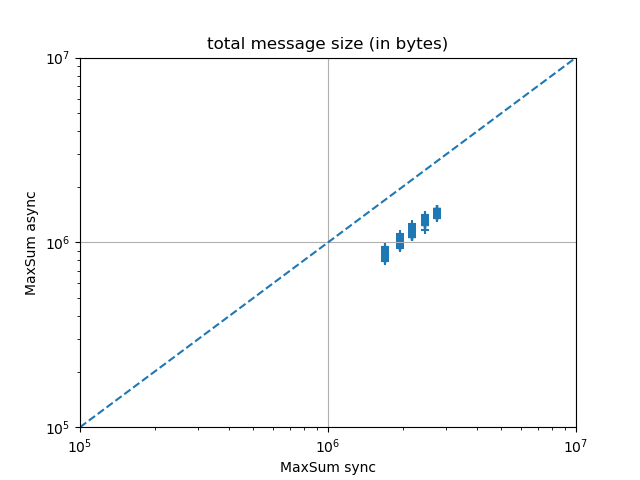
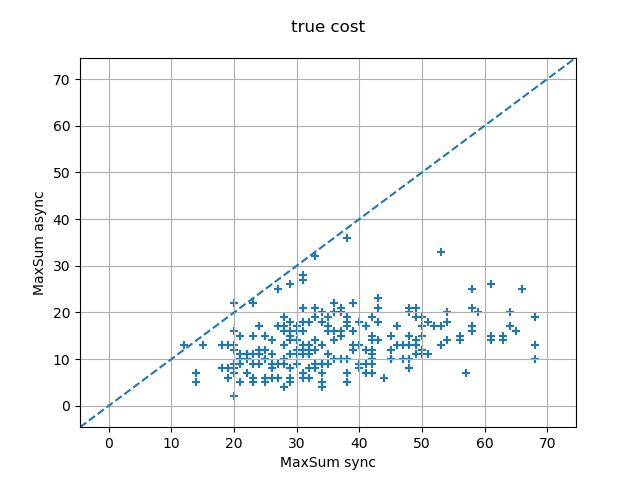
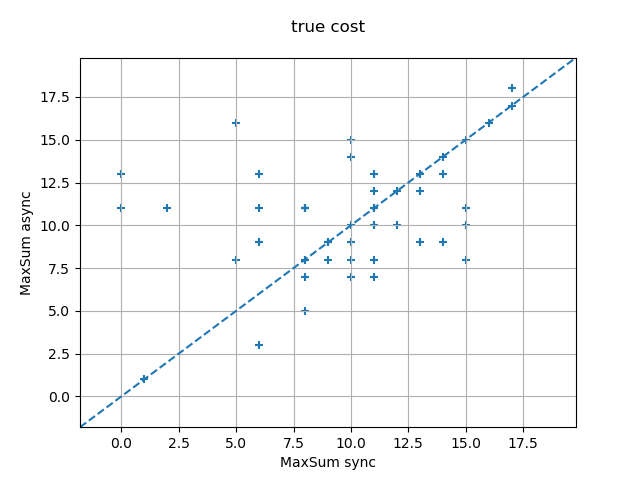
The experimental results below suggest that it is always the last phenomenon that wins over the first two, and that Max-Sum async systematically outperforms Max-Sum sync.
Graph coloring
The following experimental results were obtained on random graph coloring problems of varying sizes from 15 to 19 nodes, with a density of 0.4 and 3 colors, formulated as extensional Max-DisCSPs, and solved by 200 iterations of Max-Sum with random perturbations to break value symmetries in the optimal solutions.
Random Max-DisCSPs
The following experimental results were obtained on random Max-DisCSPs with 10 variables of domain size 10, with a density of 0.4 and a tightness varying between 0.4 and 0.99, solved by 200 iterations of Max-Sum using the JaCoP parser.
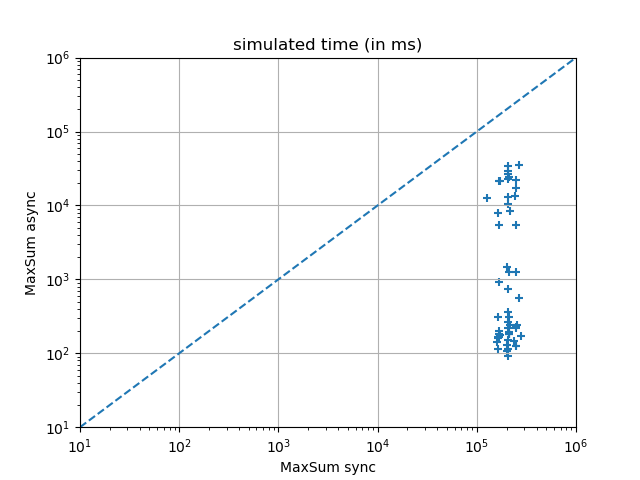
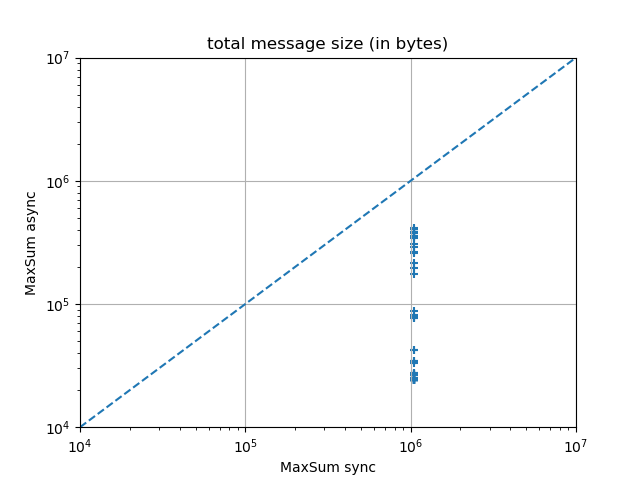
Meeting Scheduling
The following experimental results were obtained on random meeting scheduling problems with a pool of 3 agents, a number of meetings varying between 1 and 6, each meeting involving 2 agents, to be scheduled over 8 time slots, each time slot being assigned a random cost between 0 and 10 by each agent. The problem instances were formulated as DCOPs with constraint violation penalties of 1000, using the Private Events As Variables (PEAV) formulation, and solved with 200 iterations of Max-Sum with random perturbations to break value symmetries in the optimal solutions.